이진 트리란?
이진 트리는 트리의 한 종류로 각 노드가 최대 두 개의 자식 노드를 가지는 트리이다. 이진 트리는 구조에 따라 다양한 종류로 나뉘게 된다. 기본적인 트리에 대한 설명은 전 포스팅을 참고하기 바란다.
2024.06.22 - [CS/자료구조] - [자료구조] 트리 (Tree)
[자료구조] 트리 (Tree)
트리란?트리는 노드들로 구성된 자료구조로, 주로 계층적 구조를 표현하는 데 사용한다. 노드들간에 부모-자식 관계를 통해 트리를 구성한다.위 그림에서 선으로 연결된 관계를 부모-자식 관계
junote.tistory.com
이진 트리의 종류

- 완전 이진 트리 (Complete Binary Tree): 트리의 마지막을 제외한 레벨이 꽉 차 있으며, 마지막 레벨은 왼쪽부터 채워져 있는 트리이다.
- 정 이진 트리 (Full Binary Tree): 모든 노드가 0개 또는 2개의 자식 노드를 가지는 트리이다.

- 포화 이진 트리 (Perfect Binary Tree): 모든 레벨이 완전히 채워져 있는 트리로, 모든 말단 노드가 같은 깊이를 가진다.

- 이진 탐색 트리 (Binary Search Tree, BST): 왼쪽 자식 노드는 항상 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 큰 값을 가지는 트리이다.

- 편향 이진 트리 (Skewed Binary Tree): 같은 높이의 이진 트리 중에 노드의 수가 가장 적은 이진 트리를 말한다. 왼쪽 및 오른쪽 이진 트리가 있다.

- 스레드 이진 트리 (Thread Binary Tree): 스레드 이진 트리의 노드는 일반적인 이진트리와 달리 boolean 타입의 LeftThread영역과 RightTread영역을 추가로 갖는다. 노드가 말단 노드인 경우 LeftThread영역과 RightTread영역이 true가 되고 LeftChild영역은 중위순회의 선행자를 가리키게 되고 RightChild영역은 중위 후속자를 가리킨다. 참고로 위 그림에서 맨 위에 있는 노드는 head노드로 H와G노드의 없는 중위선행자 및 중위 후속자를 가리키게 하는 역할을 한다.
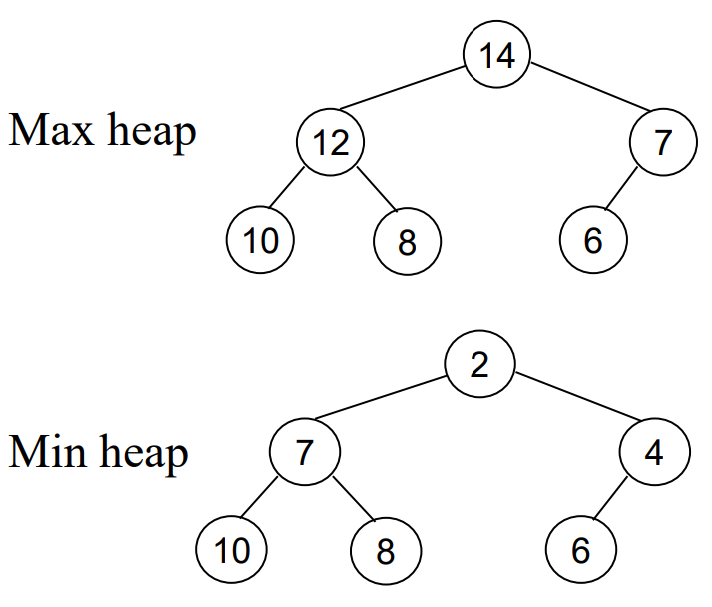
- 힙 (Heap): 여러 개의 값들 중에서 가장 크거나 작은 값을 빠르게 찾기 위해서 만든 이진 트리이다. 힙은 항상 완전 이진 트리 형태이어야 한다. 부모의 값은 항상 자식의 값보다 크거나(Max heap: 최대 힙), 작아야(Min heap: 최소 힙)한다. 따라서 루트노드에는 항상 데이터들 중 가장 큰 값(혹은 작은 값)이 저장되어 있기 때문에, 최댓값(혹은 최솟값)을 O(1)의 시간복잡도 안에 찾을 수 있다.
이진 트리의 연산
- 탐색 (Search): 특정 값을 찾는 연산이다. 시간 복잡도는 O(log n)
- 삽입 (Insertion): 새로운 값을 추가하는 연산이다. 시간 복잡도는 O(log n)
- 삭제 (Deletion): 특정 값을 제거하는 연산이다. 시간 복잡도는 O(log n)
- 중위 순회 (In-order Traversal): 왼쪽 자식 -> 부모 노드 -> 오른쪽 자식 순으로 순회한다. 이 순회를 사용하면 이진 탐색 트리에서 값이 정렬된 순서로 출력된다. LVR(Left -> Visit -> Right)
- 전위 순회 (Pre-order Traversal): 현재 노드 -> 왼쪽 자식 -> 오른쪽 자식 순으로 순회한다. VLR(Visit -> Left -> Right)
- 후위 순회 (Post-order Traversal): 왼쪽 자식 -> 오른쪽 자식 -> 현재 노드 순으로 순회한다. LRV(Left -> Right -> Visit)
- 레벨 순회 (Level-order Traversal): 루트 노드를 먼저 탐색한 후 다음 레벨의 노드를 탐색하는 방식으로 순회한다. 넓이 우선 탐색(BFS)이다.
트리의 순회 예시
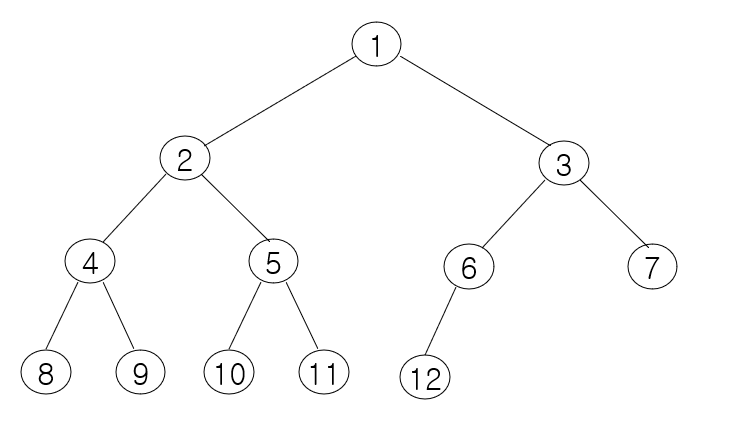
위 이진 트리에 대해서 각각의 순회를 시행해 보면 결과는 다음과 같다.

- 중위 순회(In-order Traversal): 8-4-9-2-10-5-11-1-12-6-3-7
- 전위 순회 (Pre-order Traversal): 1-2-4-8-9-5-10-11-3-6-12-7
- 후위 순회 (Post-order Traversal): 8-9-4-10-11-5-2-12-6-7-3-1
- 레벨 순회 (Level-order Traversal): 1-2-3-4-5-6-7-8-9-10-11-12
궁금한 것이나 잘못된 것이 있다면 댓글에 남겨주세요!
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 그래프 (Graph) (0) | 2024.06.26 |
|---|---|
| [자료구조] 이진 탐색 트리 (Binary Search Tree) 구현 (JAVA) (0) | 2024.06.24 |
| [자료구조] 트리 (Tree) (0) | 2024.06.22 |
| [자료구조] 연결 리스트 (Linked-List) 구현 (JAVA) (0) | 2024.06.20 |
| [자료구조] 연결 리스트 (Linked-List) (0) | 2024.06.18 |