JUNOTE

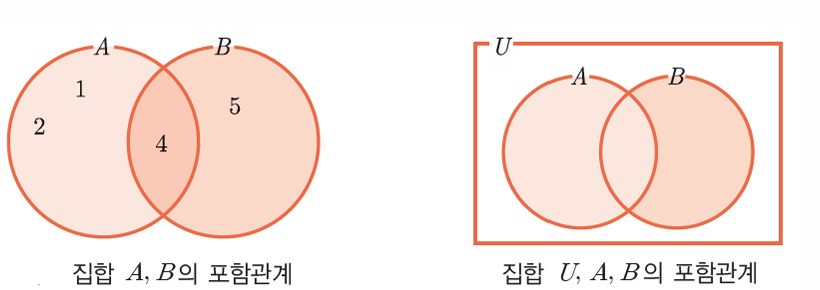
함수의 개념함수: 집합 A에서 집합 B로 가는 관계가 성립할 때, 집합 A의 원소 a에 대하여 집합 B의 원소 b 하나가 대응되는 관계를 말한다.원상: 집합 B의 원소 b와 대응하는 집합 A의 원소 a를 말한다.상: 집합 A의 원소 a에 대응하는 집합 B의 원소 b를 말한다.정의역: 원상의 집합, 집합 A를 말한다.공역: 상이 포함된 집합, 집합 B를 말한다.치역: 상의 집합, 집합 B의 부분집합, ran(f) = {f(a) | a ∈ A} 관계와 함수의 차이관계: 집합 A(정의역)의 어떤 원소는 집합 B(공역)의 원소와 전혀 대응하지 않거나 하나 이상의 원소와 대응할 수 있다.함수: 집합 A(정의역)의 모든 원소는 집합 B(공역)의 원소 하나와 반드시 대응해야 한다. 함수의 성질단사 함수: 모든 x, ..

관계의 개념관계(relation: R: A→B, aRb) / 이항관계(binary relation): 집합 A, B가 있을 때 집합 A에서 집합 B로 가는 관계로, R은 A x B의 부분집합이다. a∈A, b∈B일 때, (a, b)∈R이면 aRb, (a, b) ∉ R이면 aR/b 이라고 표현한다.정의역(domain: dom(R)): 집합 A에서 집합 B로 가는 이항관계 R에 속한 순서쌍의 첫 번째 원소가 포함된 집합, 즉 집합 A를 말한다. dom(R) = {a | a ∈ A}공역(codomain: codom(R)): 집합 A에서 집합 B로 가는 이항관계 R에 속한 순서쌍의 두 번째 원소가 포함된 집합, 즉 집합 B를 말한다. codom(R) = {b | b ∈ B}치역(range: ran(R)): 집합..

고유벡터와 고유값고유벡터와 고유값: 정방행렬 A에 대해 AX = λX(X≠0)을 만족하는 X를 고유벡터, 스칼라 λ를 고유값이라고 한다.의미1: 벡터 x에 대해 n 차 정방행렬 A를 곱하는 결과와 상수 λ를 곱하는 결과는 같다라는 의미이다.의미2: 행렬의 곱의 결과가 원래 벡터와 방향은 같고, 배율만 상수 λ 만큼만 비례해서 변했다는 의미이다. λ가 고유값이 되기 위해서는 역행렬 (λI –A)-1가 존재하지 않아야 한다. X 벡터가 0 (자명해)이 아닌 해를 갖기 위해서는 det(λI –A) ＝ 0이어야 한다. det(λI–A)를 A의 특성방정식이라 하고, 방정식을 만족하는 스칼라 λ 를 A의 고유값이라고 한다. 고유벡터와 고유값의 기하학적 의미 AX ＝λX (X=(x,y)T)우변식 λX 입장에서 해석:..

연립일차방정식의 행렬 표현해와 해집합: 일차방정식에 포함된 n개의 변수에 대응하는 값으로, 방정식을 참(T)으로 만드는 값과 그 값의 집합을 말한다.연립일차방정식: m개의 일차방정식으로 구성된 방정식을 말한다.계수행렬: 연립일차방정식의 계수들로 구성된 m x n 행렬을 말한다.미지수행렬: 연립일차방정식의 미지수들로 구성된 n x 1 행렬을 말한다.상수행렬: 연립일차방정식의 상수들로 구성된 m x 1행렬을 말한다.첨가행렬: 연립일차방정식의 계수행렬 A와 상수행렬 B를 다음과 같은 형태로 구성한 행렬행 사다리꼴 행렬: 각 행의 0이 아닌 첫번째 원소가 1이고, 그 1을 포함하는 열에서 1의 아래쪽 원소가 모두 0인 행렬이다.기약 행 사다리꼴 행렬: 행 사다리꼴 행렬에서 각 행의 0이 아닌 첫 번째 원소 1을..

역행렬역행렬: 정사각행렬 A에 대하여, AB = BA = I를 만족하는 행렬 B를 역행렬이라고 한다.(I는 단위행렬)수반행렬(adjoint matrix: [Aij]T): 여인수행렬 [Aij]의 전치행렬이다.행렬식을 이용한 역행렬:예) 가역행렬(invertible matrix): 역행렬이 존재하는 행렬, 행렬식이 0이 아닌 행렬, det(A) ≠ 0인 행렬.특이행렬(singular matrix): 역행렬이 존재하지 않는 행렬, 행렬식이 0인 행렬, det(A) = 0인 행렬. 궁금한 것이나 잘못된 것이 있다면 댓글에 남겨주세요!

행렬식행렬식(determinant: det(A) 또는 |A|): n차 정사각행에 대응하는 수를 구하는 식이다.행렬식의 기하학적 의미:  2차, 3차 정사각행렬의 기본 행렬식(사러스의 법칙):예시) 행렬식의 성질행렬 A의 각 원소의 행과 열이 바뀌어도 det(A)는 변하지 않는다.행렬식에서 두 개의 행이나 열을 서로 바꾸면 부호만 변한다.행렬 A가 서로 비례하는 두 행 또는 두 열을 갖는 정방행렬이면 det(A) = 0이다.행렬식에서 특정 어느 행이나 열의 각 성분이 두 수의 합일 때, 두 개의행렬식의 합으로 나뉠수 있다. 소행렬식과 여인수 이용컴퓨터가 4차 정사각행렬 이상의 크기를 갖는 행렬에 대해서 사러스의 법칙을 통해 행렬식을 계산하기가 어렵다. n x n 행렬의 곱셈의 개수는 n!이기 때문이다. O..

행렬이란?행렬은 하나 이상의 원소를 1차원 또는 2차원의 형태로 나열한 배열을 말한다. 다음 그림은 m행 n열로 나열한 실수의 2차원 배열이다.(m > 0, n > 0)행렬의 각각 aij는 행렬의 원소(element) 또는 성분(component)이다. 행렬의 가로줄은 행(row)이고 세로줄은 열(column)이라고 한다.영행렬(zero matrix: O): 행렬의 모든 원소가 0인 행렬을 영행렬이라고 한다.n차 정사각행렬(n-square matrix) 또는 정방행렬: m x n 행렬에 대하여 m = n인 행렬을 정사각행렬이라고 한다.주대각원소(main diagonal element): 행렬의 원소 aij 중 i = j인 원소를 주대각원소라고 한다. 즉, 행렬의 왼쪽 위에서부터 오른쪽 아래까지 이어지는 ..

집합이란?집합이란 공통적인 성질을 가진 객체들의 모임이다. 집합의 개념은 수학의 모든 분야에 있어서 기초가 될 뿐만 아니라 일상생활에서도 많이 사용하는 개념으로 현대 수학의 가장 중요한 개념이라고 할 수 있다. 먼저 집합에서 쓰이는 용어들의 정의에 대해서 알아보자.집합(set): 명확한 기준에 따라 동통 성질을 가지며 중복되지 않는 원소(element 또는 member)의 모임이다. 대문자 A, B, C등으로 표시한다.유한집합(finite set): 집합을 구성하는 원소의 개수가 유한개인 집합이다.무한집합(infinite set): 집합을 구성하는 원소의 개수가 무한히 많은 집합이다.원소(element 또는 member): 집합을 구성하는 객체이다. 소문자 a,b,c,...등으로 표시한다.기수(cardi..

증명이란?증명은 가정에서 논리적 법칙을 이용하여 결론을 이끌어내는 것을 말한다. 이때 추론이 참이면 진위 추론이라 하고, 추론이 거짓이면 허위 추론이라 한다. 그리고 별도의 증명 없이도 항상 참(T)이라고 판단되는 명제를 공리라고 한다.증명의 방법에는 대표적으로 직접 증명볍, 간접 증명볍, 수학적 귀납법이 있다. 증명을 이해하는 데에는 명제와 논리에 대한 이해가 필요하다. 이에 대한 부분은 전 포스팅을 참고하기 바란다.2024.06.28 - [수학/이산수학] - [이산수학] 명제와 논리 [이산수학] 명제와 논리논리연산자논리곱(conjunction, AND, ∧): 명제 p, q에 대해서 'p 그리고 q'를 의미한다. 명제 p, q 모두 참(T)일 때만 결과가 참(T)인 연산이다.논리합(disjunctio..

논리연산자논리곱(conjunction, AND, ∧): 명제 p, q에 대해서 'p 그리고 q'를 의미한다. 명제 p, q 모두 참(T)일 때만 결과가 참(T)인 연산이다.논리합(disjunction, OR, ∨):  명제 p, q에 대해서 'p 또는 q'를 의미한다. 명제 p, q 중 하나라도 참(T)이면 결과가 참(T)인 연산이다.부정(negation, NOT, ￢): 참(T)인 명제를 거짓(F)으로, 또는 그 반대로 바꾸는 연산이다.배타적 논리합(exclusive or, XOR, ⊕): 두 명제 p, q의 진리값 중 하나만 참(T)일 때 결과가 참이고, 그 외에는 모두 결과가 거짓인 연산이다. p ⊕ q ≡ (￢p ∧ q) ∨ (p ∧￢q)이다. ≡는 논리적 동치라는 의미이다.논리 함축(impli..