행렬식
- 행렬식(determinant: det(A) 또는 |A|): n차 정사각행에 대응하는 수를 구하는 식이다.
- 행렬식의 기하학적 의미:


- 2차, 3차 정사각행렬의 기본 행렬식(사러스의 법칙):

예시)
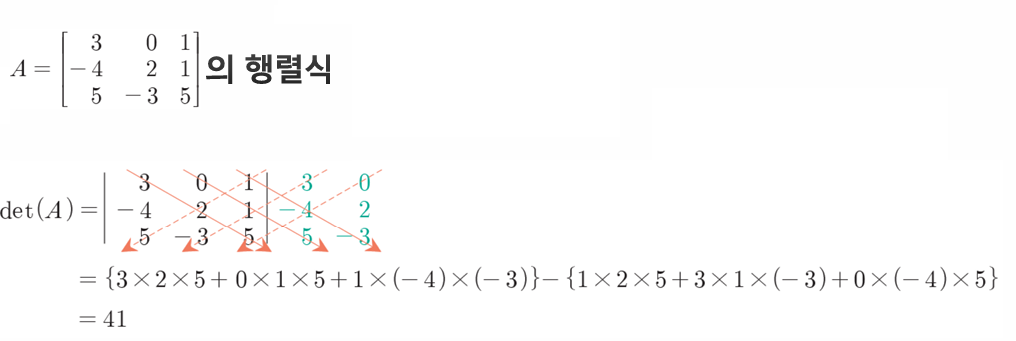
행렬식의 성질
- 행렬 A의 각 원소의 행과 열이 바뀌어도 det(A)는 변하지 않는다.

- 행렬식에서 두 개의 행이나 열을 서로 바꾸면 부호만 변한다.

- 행렬 A가 서로 비례하는 두 행 또는 두 열을 갖는 정방행렬이면 det(A) = 0이다.

- 행렬식에서 특정 어느 행이나 열의 각 성분이 두 수의 합일 때, 두 개의행렬식의 합으로 나뉠수 있다.

소행렬식과 여인수 이용
컴퓨터가 4차 정사각행렬 이상의 크기를 갖는 행렬에 대해서 사러스의 법칙을 통해 행렬식을 계산하기가 어렵다. n x n 행렬의 곱셈의 개수는 n!이기 때문이다. O(n!)의 시간복잡도는 매우 좋지 않은 시간복잡도이다. 따라서 행렬식을 소행렬식과 여인수를 이용하여 계산하는 방법을 알아야 한다.
- 소행렬: n차 정사각행렬에서 i행과 j열을 제거해서 얻은 (n-1) x (n-1) 행렬이다. n차 정사각행렬의 소행렬은 n의 제곱만큼의 개수가 만들어질 수 있다.

위 사진의 행렬 A에서는 4차 정사각행렬이므로 총 16개의 소행렬을 얻을 수 있다.
- 소행렬식: n차 정사각행렬의 소행렬 Mij의 행렬식
- 여인수(cofactor: Aij): n차 정사각행렬 A=[aij]에서 원소 aij에 관한 계수
- 여인수행렬: 여인수를 원소로 같는 행렬이다. Aij = (-1)^(i+j)det(Mij)
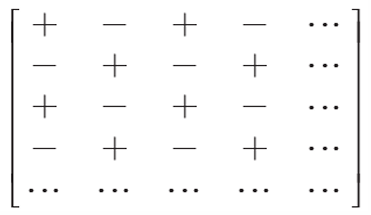
- 여인수를 이용한 행렬식: n >= 3인 n차 정사각행렬 A의 행렬식은 다음과 같다.

궁금한 것이나 잘못된 것이 있다면 댓글에 남겨주세요!
'수학 > 이산수학' 카테고리의 다른 글
| [이산수학] 행렬과 연립일차방정식 (0) | 2024.07.02 |
|---|---|
| [이산수학] 역행렬 (0) | 2024.07.02 |
| [이산수학] 행렬 (0) | 2024.07.01 |
| [이산수학] 집합 (2) | 2024.06.30 |
| [이산수학] 증명 (0) | 2024.06.30 |