함수의 개념
- 함수: 집합 A에서 집합 B로 가는 관계가 성립할 때, 집합 A의 원소 a에 대하여 집합 B의 원소 b 하나가 대응되는 관계를 말한다.
- 원상: 집합 B의 원소 b와 대응하는 집합 A의 원소 a를 말한다.
- 상: 집합 A의 원소 a에 대응하는 집합 B의 원소 b를 말한다.
- 정의역: 원상의 집합, 집합 A를 말한다.
- 공역: 상이 포함된 집합, 집합 B를 말한다.
- 치역: 상의 집합, 집합 B의 부분집합, ran(f) = {f(a) | a ∈ A}
- 관계와 함수의 차이
- 관계: 집합 A(정의역)의 어떤 원소는 집합 B(공역)의 원소와 전혀 대응하지 않거나 하나 이상의 원소와 대응할 수 있다.
- 함수: 집합 A(정의역)의 모든 원소는 집합 B(공역)의 원소 하나와 반드시 대응해야 한다.

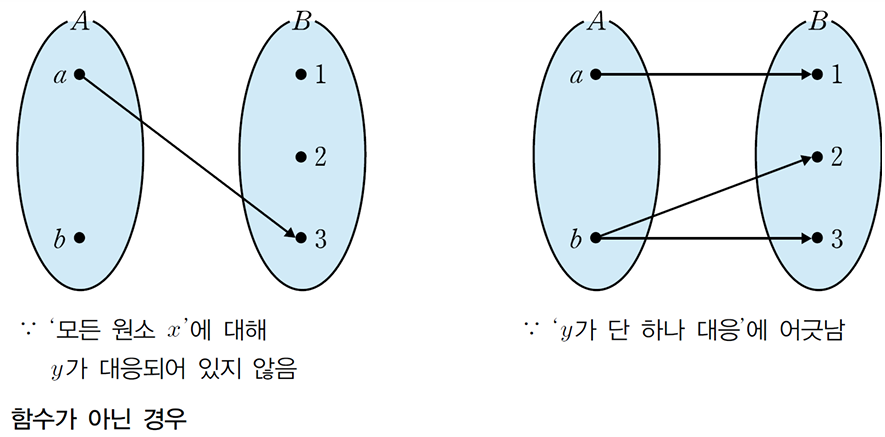
함수의 성질
- 단사 함수: 모든 x, y ∈ A에 대해서 x ≠ y이면 f(x) ≠ f(y)인 함수이다. (x1, y) ∈ f이고 (x2, y) ∈ f이면 x1 = x2이다.
- 전사 함수: f(A) = B인 함수이다. 즉, Ran(f) = B이다. ∀y ∈ B, ∃x ∈ A, y = f(x)이다. 치역과 공변역이 같아지는 함수이다.
- 전단사 함수: 단사 함수이면서 전사 함수인 함수를 말한다. 전단사 함수가 되기 위해서는 정의역의 원소 개수와 공역의 원소 개수가 같아야 하고 서로 다른 정의역 원소가 서로 다른 공역 원소와 대응해야 한다.
합성함수
- 합성함수: 두 함수 f: A → B와 g: B → C가 있을 때, 집합 A의 각 원소를 집합 C의 원소에 대응하는 함수이다. g ○ f = (g ○ f)(x) = g(f(x)), x ∈ A

- 합성함수의 성질
- f와 g가 단사함수이면, g ○ f도 단사함수이다.
- f와 g가 전사함수이면 g ○ f도 전사함수이다.
- f와 g가 전단사함수이면 g ○ f도 전단사함수이다.
- g ○ f가 단사함수이면, f도 단사함수이다.
- g ○ f가 전사함수이면, g도 전사함수이다.
- g ○ f가 전단사함수이면, f는 단사함수이고 g는 전사함수이다.
함수의 종류
- 항등함수(IA): 집합 A에 대한 함수 f: A → A가 f(a) = a로 정의되는 관계이다. 함수의 정의역, 공역, 치역 모두 상등하며 단사함수, 전사함수, 전단사함수 모두 만족한다.
- 항등함수의 합성: 함수 f: A → B가 있고 집합 A에 대한 항등함수가 IA, 집합 B에 대한 항등함수가 IB일 때, f ○ IA = IB ○ f = f
- 역함수(f-1): 전단사함수 f: A → B에 대해 B → A로 대응되는 관계 a ∈ A, b ∈ B에 대해 f(a) = b일 때, f-1(b) = a이다. (f(a): 가역함수, f-1(b): 역함수)
- 가역함수: 전단사함수로 역함수가 존재하는 함수를 말한다. 단사함수이거나 전사함수인 경우, 역함수를 구할 수 없다.
- 항등함수와 역함수의 관계: 전단사함수 f: A → B에 대하여 다음이 성립한다.
f-1 ○ f = IA
f ○ f-1 = IB
- 합성함수의 역함수: 전단사함수 f: A → B, g: B → C에 대하여 다음이 성립한다.
(g ○ f)-1 = f-1 ○ g-1
- 상수함수: 함수 f: A → B에서 집합 A의 모든 원소가 집합 B의 원소 하나에만 대응하는 관계를 말한다. ∀a ∈ A, ∃b ∈ B에 대해 f(a) = b

- 특성함수(fA): 전체집합 U의 부분집합인 A에 대하여 다음과 같은 출력을 같는 함수를 말한다.

- 바닥함수 또는 최대정수함수:

- 천장함수 또는 최소정수함수:

궁금한 것이나 잘못된 것이 있다면 댓글에 남겨주세요!
'수학 > 이산수학' 카테고리의 다른 글
| [이산수학] 관계 (0) | 2024.07.03 |
|---|---|
| [이산수학] 고유벡터와 고유값 (0) | 2024.07.02 |
| [이산수학] 행렬과 연립일차방정식 (0) | 2024.07.02 |
| [이산수학] 역행렬 (0) | 2024.07.02 |
| [이산수학] 행렬식 (0) | 2024.07.02 |