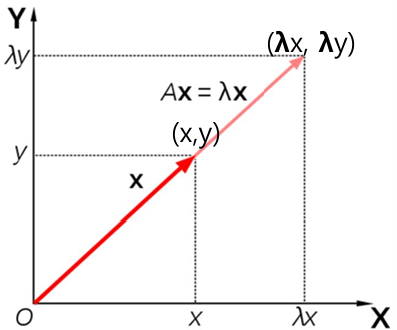
고유벡터와 고유값고유벡터와 고유값: 정방행렬 A에 대해 AX = λX(X≠0)을 만족하는 X를 고유벡터, 스칼라 λ를 고유값이라고 한다.의미1: 벡터 x에 대해 n 차 정방행렬 A를 곱하는 결과와 상수 λ를 곱하는 결과는 같다라는 의미이다.의미2: 행렬의 곱의 결과가 원래 벡터와 방향은 같고, 배율만 상수 λ 만큼만 비례해서 변했다는 의미이다. λ가 고유값이 되기 위해서는 역행렬 (λI –A)-1가 존재하지 않아야 한다. X 벡터가 0 (자명해)이 아닌 해를 갖기 위해서는 det(λI –A) = 0이어야 한다. det(λI–A)를 A의 특성방정식이라 하고, 방정식을 만족하는 스칼라 λ 를 A의 고유값이라고 한다. 고유벡터와 고유값의 기하학적 의미 AX =λX (X=(x,y)T)우변식 λX 입장에서 해석:..